Lanţ = este o secvenţă de noduri ale unui graf neorientat G=(V,E), cu proprietatea că oricare două noduri consecutive din secventa lant  sunt adiacente:

 L=[w₁, w₂, w₃,. . ,w_n]  cu proprietatea că (w_i, w_i+1)ÎE pentru  1£i<n.

Lungimea unui lanţ = numărul de muchii din care este format.

Lanţ simplu = lanţul care conţine numai muchii distincte

Lanţ compus= lanţul care nu este format numai din muchii distincte

Lanţ elementar = lanţul care conţine numai noduri distincte

Ciclu = Un lanţ în care primul nod coincide cu ultimul.

Ciclul este elementar dacă este format doar din noduri distincte, excepţie făcând primul şi ultimul. Lungimea unui ciclu nu poate fi 2.

Graf partial = Dacă dintr-un graf G=(V,E) se suprimă cel puţin o muchie atunci noul graf G’=(V,E’), E’Ì E se numeşte graf parţial al lui G (are aceleasi noduri si o parte din muchii).

 Subgraf = Dacă dintr-un graf G=(V,E) se suprimă cel puţin un nod împreună cu muchiile incidente lui, atunci noul graf G’=(V’,E’), E’Ì E si V’ÌV se numeşte subgraf al lui G.

Graf regulat = graf neorientat în care toate nodurile au acelaşi grad;

Graf complet = graf neorientat G=(V,E) în care există muchie între oricare două noduri.

Numărul de muchii ale unui graf complet este:  nr*(nr-1)/2.Unde nr este numarul de noduri

graf complet. Nr de muchii: 4x(4-1)/2 = 6

Graf conex = graf neorientat G=(V,E) în care pentru orice pereche de noduri (v,w) există un lanţ care le uneşte.

graf conexnu este graf conex

Componentă conexă = subgraf al grafului de referinţă, maximal în raport cu proprietatea de conexitate (între oricare două vârfuri există lanţ);

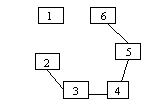
graful nu este conex. Are 2 componente conexe:

                                                1, 2 si 3, 4, 5, 6

Lanţ hamiltonian = un lanţ elementar care conţine toate nodurile unui graf

 L=[2 ,1, 6, 5, 4, 3] este lant hamiltonian

Ciclu hamiltonian = un ciclu elementar care conţine toate nodurile grafului

C=[1,2,3,4,5,6,1] este ciclu hamiltonian

Graf hamiltonian = un graf G care conţine un ciclu hamiltonian

Graful anterior este graf Hamiltonian.

Daca G este un graf cu n>=3 noduri astfel incat gradul fiecarui nod este mai mare sau egal decat n/2 atunci G este hamiltonian

Lanţ eulerian = un lanţ simplu care conţine toate muchiile unui graf

Lantul: L=[1.2.3.4.5.3.6.2.5.6] este lant eulerian

Ciclu eulerian = un ciclu simplu care conţine toate muchiile grafului

 Ciclul: C=[1.2.3.4.5.3.6.2.5.6.1] este ciclu eulerian

Graf eulerian = un graf  care conţine un ciclu eulerian.

                                    Intrebari si exercitii :

1. desenati un graf G neorientat cu 6 noduri si 10 muchii
2. Exprimati graful ca o relatie binara detaliind multimea nodurilor si multimea muchiilor
3. precizati pentru fiecare nod gradul
4. precizati un lant simplu, un lant compus
5. precizati un lant elementar, neelementar
6. precizati un ciclu
7. desenati un graf Gp partial cu 7 muchii
8. desenati un subgraf Gs cu 4 noduri
9. modificati Gs astfel incat Gs sa fie graf complet
10. desenati un graf regulat Gr cu 9 noduri
11. cate componente conexe are Gr?
12. modificati Gr astfel incat sa obtineti Gr1 graf conex
13. precizati un lant hamiltonian in Gr1
14. modificati  Gr astfel incat acesta sa fie graf eulerian
15. precizati un ciclu eulerian in Gr
16. puteti desena urmatoarea figura fara a ridica creionul de pe hartie si fara a repete muchiile?

17. este graful anterior eulerian ? de ce ?

Pentru inceput un scurt istoric despre parintii teoriei grafurilor:
Leonard Euler

STIATI CA...

Leonard Euler este considerat a fi fost forta dominanta a matematicii secolului al XVIII-lea si unul dintre cei mai remarcabili matematicieni si savanti multilaterali ai omenirii. El a introdus notiunea de functie si a fost primul care a notat f(x) pentru aplicarea functiei f elementului x.
De asemenea, el a introdus notatia moderna pentru functiile trigonometrice, litera e pentru baza logaritmului natural (cunoscut in prezent drept numarul lui Euler), litera greceasca ? pentru suma si litera i pentru unitatea imaginara.
Folosirea literei grecesti ? pentru raportul dintre circumferinta unui cerc si diametrul sau a fost de asemenea popularizata de Euler, chiar daca ideea nu a pornit de la el. 
 
Primele notiuni in teoria grafurilor ca parte integranta a matematicii au fost definite in anul 1736 de catre Leonhard Euler .
Problema pe care a rezolv-o si care a dus la noi fundamente teoretice in teoria grafurilor este o problema practica legata de traversarea celor 7 poduri din Königsberg - Prusia, plecand de la un pod si trecand prin celelalte o singura data , intorcandu-se la podul de pornire.
Arthur Cayley

STIATI CA...

Arthur Cayley s-a nascut în Londra. Tatal sau, Henry Cayley, a fost var cu Sir George Cayley, inventator în domeniul aeronauticii.
În 1852, Francis Guthrie a incercat sa coloreze o harta reprezentand comitatele Angliei, astfel incat doua regiuni cu frontiera comuna sa aiba culori distincte.
De cate culori este nevoie pentru a colora o harta oarecare, astfel incat regiunile cu frontiera comuna sa aiba culori diferite?
De la profesor la student, de la coleg la coleg… problema a ajuns la Arthur Cayley, care i-a intrebat pe colegii sai din London Mathematical Society.
S-a demonstrate ca sunt suficiente 4 culori care sa resolve aceasta problema.

Conceptul de graf chimic a fost formulat de matematicianul britanic Arthur Cayley inaintea introducerii termenului graf.
O contributie importanta in studiul grafurilor chimice o are chimistul roman Alexandru T. Balaban 

Variantele 31-39

Varianta 31: Se considera graful neorientat cu 7 noduri, numerotate de la 1 la 7, si muchiile[1,3],[2,3], [3,4], [3,5], [5,4], [1,2], [2,5], [2,4], [6,7], [3,6]. Care dintre urmatoarele succesiuni de noduri reprezinta un lant care trece o singura data prin toate nodurile grafului? (4p.)

   
a. (1, 2, 3, 4, 5, 6, 7)                

b. (4, 5, 3, 6, 7)

c. (7, 6, 3, 5, 4, 2, 1)               

d. (1, 3, 5, 4, 2, 3, 6)

  

Raspuns :  c ,deoarece este singura succesiune de noduri  care trece o singura data prin toate varfurile.

Varianta 32. Graful neorientat cu 8 noduri, numerotate de la 1 la 8, este

reprezentat cu ajutorul matricei de adiacenta alaturate.  Pentru acest graf este adevarata afirmatia: (4p.)

a. Graful este hamiltonian               

b. Graful nu are noduri de grad 0

c. Gradul maxim al unui nod este 3

d. Graful are trei componente conexe

Raspuns:d ,deoarece  graful nu contine toate nodurile conditie necesara pentru un graf hamiltonian, are graduri de nodul 0 iar gradul maxim al unui nod este 4. Dupa cum se poate observa pe desenul corespunzator matricei de adiacenta graful are 3 componente conexe.

Varianta 34. Graful neorientat cu 60 de noduri, numerotate de la 1 la 60, are numai muchiile [1,60], [60,20], [2,30] si [4,30]. Numarul componentelor conexe ale grafului este egal cu:

(4p.)

a. 3

b. 56

c. 54 

d. 0

 Raspuns b. deoarece din 60 de noduri scadem 6 noduri si adaugam 2(cele 2 componente conexe) rezultand 56.

Varianta 35. Un graf neorientat cu 10 noduri, numerotate de la 1 la 10,este reprezentat cu ajutorul listelor de adiacenta alaturate.Câte componente conexe are graful si care este numarul    minim de muchii ce trebuie adaugate pentru ca graful sa fie

conex? (6p.)

1:3,5

2:4

3:1,5

4:2,8

5:1,3

6:

7:10

8:4

9:

10:7

Raspuns :5 componente conexe  ,                                           trebuie adaugate 4  muchii astfel  incat graful sa fie conex.

Varianta 36. Se considera un graf neorientat cu 7 noduri       numerotate de la 1 la 7 si muchiile [1,2],[1,3],[2,3],[2,4],[2,5],[2,6],[4,6],[5,7],[6,7]. Care este numarul minim de muchii care trebuie adaugate pentru ca acest graf sa devina eulerian? (4p.)

Raspuns : minim 8 muchii(muchiile albastre) (fiecare nod trebuie sa aiba grad par si trebuie sa existe toate muchiile )

Varianta 38. Urmatorii doi itemi se refera la un graf neorientat cu 7 noduri,nume-rotate de la 1 la 7 si muchiile [1,5], [2,3], [2,4], [2,5], [3,4], [4,5], [4,7], [5,6], [5,7].

1. Care este numarul minim de muchii care trebuie eliminate astfel încât graful sa aiba 3 componente conexe? (6p.)

Raspuns:eliminam [1,5] [5,6] (2 muchii ) si avem 1 si 6 doua componenta conexe   {2,3,4,5,7} formeaza a treia componenata conexa .

2. Câte cicluri elementare distincte exista în graf? Doua cicluri sunt distincte daca difera prin cel putin o muchie.

Raspuns: 5 cicluri elementare

Rezolvare :

(2,5,7,4,3,2)  

(2,3,4,2)

(3,4,5,2,3)

(3,2,5,7,4,3)

(3,2,4,7,5,3)

Varianta 39. Se considera un graf neorientat cu 8 noduri, numerotate de la 1 la 8, si muchiile [1,5], [1,6], [2,6], [3,4], [3,6], [3,7], [4,6], [6,8], [7,8]. Daca se elimina nodul 6 si toate muchiile incidente cu acesta câte componente conexe va avea subgraful rezultat?

                                                                                         
 Rezolvare:

Raspuns : 3 componenete conexe 

Problema Rezolvate

Variante Bac 51-59 P.B                                                       Varianta 51

2) Se consideră un graf neorientat cu 5 noduri şi 9 muchii. Care dintre următoarele şiruri de

numere pot fi gradele nodurilor grafului?

a) 4, 2, 6, 4, 2                  b) 2, 2, 1, 2, 2

c) 1, 1, 1, 1, 1                  d) 4, 3, 3, 4, 4

                                          


Raspuns:se foloseste formula 2*m=2*9=18,d) este varianta corecta.

  

Probleme rezolvate

Probleme rezolvate


1.

Matricea lanturilor - algoritmul Roy-Warshall Se citeste un graf neorientat cu n noduri si m muchii dat prin vectorul muchiilor. Sa se construiasca o matricea existentei lanturilor(a[i][j] este 1 daca exista lant de la i la j si 0 in caz contrar). Ex: Pentru graful din imagine se obtine matricea lanturilor urmatoare: 0 0 1 1 1 1 0 0 0 0 0 0 1 0 0 1 1 1 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 1 0

#include<fstream.h>
int k,m,n,x[100],a[100][100],p[100];

fstream f("graf.in",ios::in);
fstream g("graf.out",ios::out);

void citire()
 {int x,y;
  f>>n>>m;
  for(int i=1;i<=m;i++)
   {f>>x>>y;
    a[x][y]=1;
    a[y][x]=1;
   }
 }
void rw()
 {int i, j, k;
  for(k=1;k<=n;k++)
   for(i=1;i<=n;i++)
    for(j=1;j<=n;j++)
   if(i!=j)
   if(a[i][j]==0)
   a[i][j]=a[i][k]*a[k][j];
 }
 void afis()
  {for(int i=1;i<=n;i++)
    {g<<endl;
     for(int
     j=1;j<=n;j++)
      g<<a[i][j]<<" ";
   }
  }

 void main()
  {citire();
   rw();
   afis();
  }

2.

Se da un graf neorientat cu n varfuri si m muchii, citit prin vectorul muchiilor. Sa se afiseze pe linii separate componentele sale conexe. 
Ex: Pentru graful alaturat se vor afisa urmatoarele componente conexe: 
1 2 4 5 
3 7 
6

#include<fstream.h>

int a[100][100],n,m,x[100],p[100];

void citire()
{ int i,l,c;
  ifstream f("g.in");
  f>>n>>m;
  for(i=1;i<=m;i++)
  { f>>l>>c;
    a[l][c]=1;
    a[c][l]=1;
  }
}

void bf(int k)
{ int i,s,d;
  x[1]=k;
  p[k]=1;
  s=d=1;
  while(s<=d)
  { for(i=1;i<=n;i++)
     if(a[x[s]][i]==1 && !p[i])
 { d++;
   x[d]=i;
   p[i]=1;
 }
    s++;
  }
  for(i=1;i<=d;i++) cout<<x[i]<<" ";
  cout<<endl;
}

void main()
{ citire();
  int i;
  for(i=1;i<=n;i++)
    if(!p[i]) bf(i);
}